Mathematics
— Coordinate Systems
[Rectangular Coordinate System]
Cartesian
coordinate system: another name
Cartesian
coordinate system in one dimension:
a point x on a straight line. ![]()
![]()
Cartesian
coordinate system in two dimensions: a
point (x, y) on the xy-plane. ![]()
Cartesian
coordinate system in three dimensions:
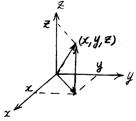
Base
vectors: ![]()
![]() : in the direction of increasing x with y and z held constant.
: in the direction of increasing x with y and z held constant.
![]() : in the direction of increasing y with z and x held constant.
: in the direction of increasing y with z and x held constant.
![]() : in the direction of increasing z with x and y held constant.
: in the direction of increasing z with x and y held constant.
They are all perpendicular to each
other:
![]()
Base vectors ![]() are constant once
they are defined.
are constant once
they are defined.
The
right-hand rule: ![]()
Coordinate
of a point: ![]()
Position
vector: a vector from (0, 0, 0) to (x, y,
z). ![]()
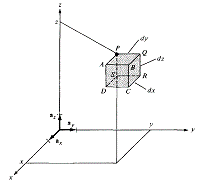
Incremental
length: ![]()
Incremental
area: ![]()
Incremental
volume: ![]()
[Cylindrical Coordinate System]
Cylindrical
coordinate system in two dimensions:
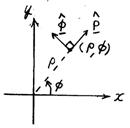
Base vectors:
![]()
Polar-to-rectangular
base vector conversion:
Since ![]() is on the
xy-plane, it can be represented by a combination of
is on the
xy-plane, it can be represented by a combination of ![]() and
and ![]() :
: ![]()
Angle between ![]() and
and ![]() :
: ![]() ¡æ
¡æ ![]()
Angle between ![]() and
and ![]() :
: ![]() ¡æ
¡æ ![]()
Thus,
![]()
Angle between ![]() and
and ![]() :
: ![]() ¡æ
¡æ ![]()
Angle between ![]() and
and ![]() :
: ![]() ¡æ
¡æ ![]()
Thus,
![]()
In summary,
![]() ,
, ![]()
Conversely we have
![]() ,
, ![]()
Coordinate of a point:
![]()
![]() : distance from (0, 0) to the point
: distance from (0, 0) to the point ![]()
![]() : angle measured in counterclockwise direction from the
positive x axis to the line segment
from (0, 0) to
: angle measured in counterclockwise direction from the
positive x axis to the line segment
from (0, 0) to ![]()
Polar-to-rectangular
coordinate conversion:
![]()
![]()
Position vector:
![]()
Cylindrical coordinate
system in three dimensions:
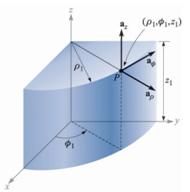
Base
vectors: ![]() . They are all perpendicular to each other. Base vectors
. They are all perpendicular to each other. Base vectors ![]() change directions
as the point moves.
change directions
as the point moves.
The
right-hand rule: ![]()
Cylindrical-to-rectangular
base vector conversion:
![]() ,
, ![]() .
.
![]() ,
, ![]() .
.
Coordinate
of a point: ![]()
Cylindrical-to-rectangular
coordinate conversion:
![]()
![]()
Position vector:
![]()
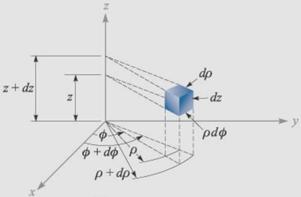
Incremental
length: ![]()
Incremental
area: ![]()
Incremental
volume: ![]()
[Spherical Coordinate System]
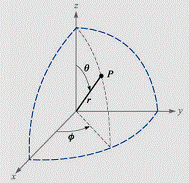
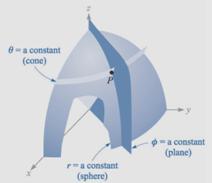
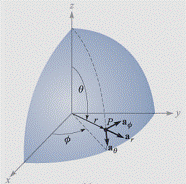
Base
vectors: ![]() . They are all perpendicular to each other. Base vectors
. They are all perpendicular to each other. Base vectors ![]() change directions as the point moves.
change directions as the point moves.
The
right-hand rule: ![]()
Spherical-to-rectangular
base vector conversion:
Angle between ![]() and
and ![]() :
: ![]() ¡æ
¡æ ![]()
Angle between ![]() and xy-plane:
and xy-plane: ![]() ¡æ
¡æ ![]()
Thus,
![]()
Angle between ![]() and
and ![]() :
: ![]() ¡æ
¡æ ![]()
Angle between ![]() and xy-plane:
and xy-plane: ![]() ¡æ
¡æ ![]()
Thus,
![]()
Angle between ![]() and
and ![]() :
: ![]() ¡æ
¡æ ![]()
Angle between ![]() and
and ![]() :
: ![]() ¡æ
¡æ ![]()
Thus,
![]()
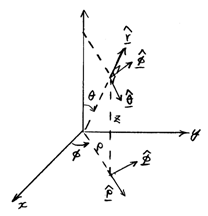
In summary,
![]()
![]()
![]()
Conversely we can obtain:
![]()
![]()
![]()
Coordinate
of a point: ![]()
Spherical-to-rectangular
coordinate conversion:
![]()
![]()
Position vector:
![]()
Incremental
length: ![]()
Incremental
area: ![]()
Incremental
volume: ![]()