실습-12 안테나의 편파(Polarization in Antennas)

 

안테나에서 방사된 전기장 벡터가 시간에 따라 변하는 궤적 형상에 따라 선형편파(수직편파, 수평편파, 경사편파, 45º 편파), 원평파(우원편파, 좌원편파), 타원편파 등으로 분류한다. 두 안테나 사이에 에너지 전달이 잘 되러면 편파가 일치해야 하며 편파 불일치에 의한 전력전달 효율을 편파손실계수라한다. 편파가 완전정합 시(예: 수직편파 대 수직편파, 우원편파 대 우원편파) 편파손실계수는 1이면, 완전 부정합시(예: 수직편파 대 수평편파, 우원편파 대 좌원편파) 편파손실계수는 0이다. 편파가 부분적으로 정합 시(예: 수직편패 대 45º 편파, 선형편파 대 원편파) 편파손실계수는 0보다 크고 1보다 작은 값을 가진다.

 

직교편파는 안테나의 편파가 서로 공간적으로 또는 시간적으로 직각이 되어 두 편파 성분 사이에 에너지 교환이 일어나지 않는 경우를 의미한다. 예로서 수직편파와 수평편파, 좌원편파와 우원편파는 서로 직교하는 편파이다. 이중편파 안테나는 1개의 안테나에 입력단자를 2개 설치하고 각 단자에서 서로 직교하는 편파를 생성하도록 한 것이다. 예를 들어 동시에 수직편파와 수평편파, 동시에 우원편파와 좌원편파를 방사하는 안테나를 이중편파 안테나라 한다. 동일한 주파수 대역을 사용하면서 수직편파로 신호 1을 송신하고 수평편파로 신호 2를 송신하므로서 주파수 이용율을 2배로 증가시킬 수 있다. 이 경우 편파 분리도 20dB 이상 높아야 한다.

 

편파 이중성(diversity)는 편파에 따라 지상 장애물이 있는 공간을 전파하는 특성이 다르므로 송신 시 직교하는 2개의 편파로 동일한 신호를 동시에 송신한 후 수신 측에서도 2개의 편파를 동시에 수신하여 더 큰 신호를 이용하는 기법이다. 지면, 산, 건물이 있는 지상에서 통신할 경우 직접파와 물체에서 반사된 파가 간섭을 일으켜 신호가 특정 수신 위치에서 감소하는 현상을 다중경로 페이딩이라 하는 데, 다중경로 페이딩 문제 대처하는 방법 중의 하나가 편파 이중성이다.

 

사용자 단말기의 선형편파 안테나 또는 물체에 부착된 태그의 선형편파 안테나가 방향이 다양하게 변화할 때 기지국(리더기)과 원활한 통신을 하기 위해 기지국에서는 신호를 이중편파 또는 원편파로 송신한다. 이온 층 밖의 인공위성 또는 우주선과 통신 시 전파의 편파가 이온층을 통과하면서 회전되기 때문에 (특정 주파수에서 심함) 원편파를 사용한다.

 

I. 실습

1. 편파정합 실습

자유공간에서

주파수: 1.15GHz, 파장 λ = 261mm

다이폴 1, 다이폴 2 치수: 도선 절반 길이 50mm, 직경 5mm, 급전 갭 10mm

다이폴 1: 중심위치 , 다이폴 도선 방향 = y 축방향

다이폴 2: 중심위치  

다이폴 급전: discrete port, 50Ω 내부 저항

1) 다이폴 2의 도선 방향 = y 축방향

a) 안테나 형상

b) 다이폴 1과 다이폴 2의 반사계수

|S11|(dB), |S22|(dB): -40dB to 0dB, 0.9-1.3GHz, 같은 그래프에

c) 전달계수

|S21|(dB): -40dB to 0dB, 0.9-1.3GHz

 

2) 다이폴 2의 도선 방향 = +y축 방향에서 +x축 방향으로 45º 회전

a) 안테나 형상

b) 전달계수

|S21|(dB): -40dB to 0dB, 0.9-1.3GHz

 

3) 다이폴 2의 도선 방향 = x축 방향

a) 안테나 형상

b) 전달계수

|S21|(dB): -200dB to 0dB, 0.9-1.3GHz

 

2. 원편파 안테나 실습

자유공간에서

주파수: 1.15GHz, 파장 λ = 261mm

다이폴 1, 다이폴 2 치수: 도선 절반 길이 50mm, 직경 5mm, 급전 갭 10mm

다이폴 급전: discrete port, 50Ω 내부 저항

다이폴 1: 중심위치 , 다이폴 도선 방향 = y 축 방향, 급전전압 +y 방향이 양극, 전압크기 1, 전압위상 0º

다이폴 2: 중심위치 , 다이폴 도선 방향 = x 축 방향, 급전전압 +x 방향이 양극, 전압크기 1, 전압위상 90º

 

a) 안테나 형상

b) 다이폴 1과 다이폴 2의 반사계수

|S11|(dB), |S22|(dB): -40dB to 0dB, 0.9-1.3GHz, 같은 그래프에

c) 전달계수

|S21|(dB): -40dB to 0dB, 0.9-1.3GHz

d) 이득패턴

3D , G(RHCP), 1.15GHz

e) 이득패턴

3D, G(LHCP), 1.15GHz

f) 축비패턴

1D, Cartesian, 0dB to 20dB, phi = 45º, theta = -180º to +180º

 

II. 이론

학습자료

McMaster Unviersity, Nikolova, Lecture 5: Polarization and Related Antenna Parameters

 

1. 편파의 기초

ㅇ 편파의 분류

- 안테나에서 방사된 전기장 벡터의 시간에 따른 궤적에 따라 편파를 다음과 같이 분류

    선형편파(LP, linear polarization): 직선궤적

    타원편파(EP, elliptic polarization): 타원궤적

    원편파(CP, cicular polarization): 원궤적

- 편파의 회전방향: 진행방향을 엄지로 설정, 나머지 손가락은 전기장 벡터 방향

- 우원편파: 오른손 나머지 손가락의 회전방향과 전기장 회전방향 일치

- 좌원편파: 왼손 나머지 손가락의 회전방향과 전기장 회전방향 일치

 

1. 선형편파

- 안테나에서 방사된 전기장 벡터를 분석하기 위해 지역적 직각 좌표계 설정

    +z 축: 전파가 진행하는 방향

    A, B: 전기장의 x, y 성분 진폭

 

     

     

 

https://www.mathworks.com/help/phased/ug/polarizationstates.png

그림: 선형편파 전기장 벡터 궤적

 

2. 원편파(CP, circular polarization)

- 좌원편파(LHCP, left-hand circular polarization)

     

     

     

     

 

- 우원편파(RHCP, right-hand circular polarization)

     

     

     

     

 

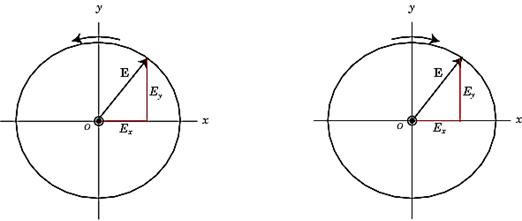
https://www.mathworks.com/help/phased/ug/polarizationstates.png

            (a)                                      (b)

그림: +z 방향으로 전파가 진행할 경우 (a) 우원편파, (b) 좌원편파

 

3. 편파타원(Polarization Ellipse)

ㅇ 타원편파(EP, elliptic polarization)

- 모든 편파를 타원편파로 표현 가능

- 일반적인 편파를 표현하기 위해 편파타원을 사용

 

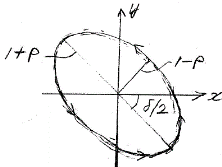
ㅇ 편파타원

     

     

     

- 전기장 벡터의 시간에 따른 궤적: 타원. 수학식 유도 복잡

 

 

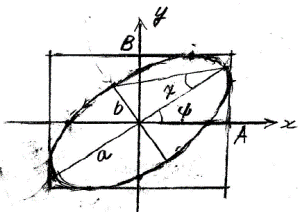
그림: 편파타원

 

 

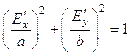
: to be used in Stokes paramter defintion

 

 

 : orientation angle

A discontinuity of π/2 exists when A = B.

δ > 0 : left-hand polarization

δ < 0 : right-hand polarization

 

: ellipticity angle

 : semi-major axis

: semi-minor axis

: axial ratio (축비)

: ellipticity or eccentricity

 

: wave properties

: polarization ellipse

 

 

 

- 편파회전 방향: 전파의 진행방향 = + z 방향

    RHCP if  

    LHCP if  

 

그림: 편파타원. . 우원편파

 

- A, B가 주어진 경우: 축비가 최소가 되는 위상차  

- 위상차 가 주어진 경우: 축비가 최소가 되는 진폭비 A/B = 1

 

ㅇ 축비(AR, axial ratio)

- 편파궤적 타원에서 장축의 길이를 단축의 길이로 나눈 값

     : axial ratio

     

- 축비 대역폭: 축비가 3dB 이하인 주파수 범위

- 선형편파 안테나의 축비: ∞

 

ㅇ 선형편파(LP, linear polarization)

1)  

   

     

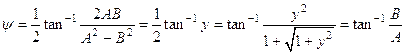
2)

   

     

 

ㅇ 원편파(CP, circular polarization)

1)

 

 

ㅇ Polarization Plane

: complex polarization ratio

 

4. 편파손실계수(PLF, Polarization Loss Factor)

ㅇ 편파벡터(polarization vector): 안테나 송신 시 정규화한 전기장 벡터: 크기 1

     

 

- 수신 시 편파벡터: 송신 시 편파벡터의 conjugate (공액복소수)

   

 

ㅇ 편파손실계수

- 안테나 1 편파벡터 (송신 시):   

- 안테나 2 편파벡터 (송신 시):

   

 

    E1: 안테나 1의 전기장 벡터 (송신 시)

    E2: 안테나 2의 전기장 벡터 (송신 시)

     

 

- 안테나 1의 편파벡터 (송신 시):  

- 입사파의 편파벡터:  

   

 

5. 편파 구(Polarization Sphere)

- Poincaré sphere

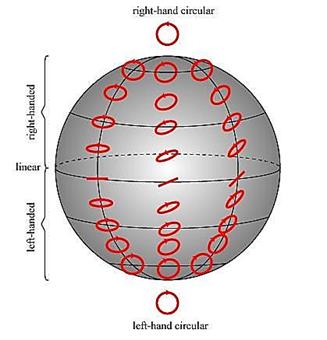
   http://cdn.shopify.com/s/files/1/1026/4509/files/poincaresphere.jpg?2690835184976070306

그림: 편파 구

 

- 편파 타원의 패러미터 를 사용하여 타원 상에 편파 타원 표시

    고각:  

    방위각:  

- 타원 상의 점  

     

- 각 점에 대응되는 편파 타원 표시: Poincaré ellipse

 

6. Polarization Representation

: RHCP

: LHCP

 

 

 

: circular polarization ratio

: phase difference between LCP and RCP components

 

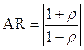
 : RCP

 : LCP

 

7. Circularly Polarized Antenna

1) Ludwig's 3rd definition

     

 

    Zero cross-polarization in the principal planes ()

    EC : horizontally polarized

    EX : vertically polarized

 

   

 

2) RCP and LCP fields of an antenna

Wave propagating in  direction

 

 

 

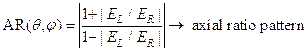
3) Polarization loss factor in terms of the axial ratio

: antenna 1, transmitting field

: antenna 2, transmitting field