Electromagnetics (전자기학)

1. 공지사항

ㅇ Grading: 출석 15% , 과제 15%, 중간시험 35%, 기말시험 35%

ㅇ Textbook: Ulaby의 전자기학 7판, 김강욱, 김남, 오이석, 이용식, 조영기, 2016년, 성진미디어

ㅇ 원서교재: Ulaby-FAE-7e.pdf, Web http://em7e.eecs.umich.edu/start_here.html

ㅇ 과제용 학생고유번호 PIN: 학교에 등록된 자신의 이동전화 끝 4자리. 단 각 숫자가 0인 경우 순차적으로 1, 2, 3, 4로 대체. 사용 예: 1C 전하로부터 PIN (m) 떨어진 점에서 전기장 세기 (V/m)를 구하라.

ㅇ 과제 제출: eCampus에 수업일 해당주 일요일 23:59이전

2. 주별 강의

01주 Introduction to Electromagnetics (pdf, pptx-no-voice, pptx-voice, mp4)

02주 Vector Calculus (pdf, pptx-no-voice, pptx-voice, mp4)

03주 Coordinate Systems (pdf, pptx-no-voice, pptx-voice, mp4)

04주: Electrostatics 1 (pdf, pptx-no-voice, pptx-voice, mp4)

05주: Electrostatics 2 (pdf, pptx-no-voice, pptx-voice, mp4)

06주: Electrostatics 3 (pdf, pptx-no-voice, pptx-voice, mp4)

07주: Electrostatics 4 (pdf, pptx-no-voice, pptx-voice, mp4)

08주: Mid-term Exam. (prob, sol) on 2021-4-19. The exam starts at 16:00, ends at 16:40.

09주: Magnetostatics 1 (pdf, pptx-no-voice, pptx-voice, mp4)

10주: Magnetostatics 2 (pdf, pptx-no-voice, pptx-voice, mp4)

11주: Maxwell's Equations 1 (pdf, pptx-no-voice, pptx-voice, mp4)

12주: Maxwell's Equations 2 (pdf, pptx-no-voice, pptx-voice, mp4)

13주: Planewave 1 (pdf, pptx-no-voice, pptx-voice, mp4)

14주: Planewave 2 (pdf, pptx-no-voice, pptx-voice, mp4)

15주: Final Exam. (prob, sol)

(Homework 01주)

1. What is the charge of an electron?

2. Write down an equation for the force between two point charges.

3. An AC voltage is given by v(t) = 10 cos(10t +20°). Write down the phasor V of v(t).

(Homework 02주)

x = 자신의 이동전화 번호 끝 4자리에서 첫숫자와 마지막 숫자를 뺀 값. 예: 3194, 3-4 = -1

4개의 벡터: a = (x, 2x, x-2), b = (2-x, -2x, x+1), c = (x, 2x, 3x), d = (5x, x+4, x-3)

1. Find p = a · b and q = a × b.

2. Find the aea of a triangle whose vertices are a, b, and c.

3. Find the volume of a tetrahedron whose vertices are a, b, c, and d.

4. Compose a python code to solve the above three problems, run the code and include the result on your homework.

(Homework 03주)

1. 자신의 이동전화 끝 4자리(PIN)를 사용하여 다음 예와 같이 a, b, c, d 생성

PIN=abcd=3194, a=3, b=1, c=9, d=4

A point in space P(x, y, z) = (a, b, c) is given.

2. Express the point in the spherical coordinate P(r, θ, φ).

3. Express the base vectors of the spherical coordinate system at P in terms of .

4. Compose a Python code to solve the above three problems, run the code and include the result in your homework.

(Homework 04주)

1. 자신의 이동전화 끝 4자리(PIN)를 사용하여 다음 예와 같이 a, b, c, d 생성

PIN = abcd = 3194, a = 3, b = 1, c = 9, d = 4

A point charge at P(x, y, z) = (b, c, d) m has charge (a + b + c + d) × 1e-9 C.

1. Find the electric field E = (E_x, E_y, E_z) V/m at a point Q(x, y, z) = (d + c, a + d, b + c) m.

2. Compose a Python code for Problem 1, run the code and include the source code and the result of code run in your homework.

(Homework 05주)

1. 자신의 이동전화 끝 4자리(PIN)를 사용하여 다음 예와 같이 a, b, c, d 생성

PIN = abcd = 3194, a = 3, b = 1, c = 9, d = 4

A point charge at P(x, y, z) = (b, c, d) m has charge (a + b + c + d) × 1e-9 C.

Find the electric potential V (V) at a point Q(x, y, z) = (d + c, a + d, b + c) m.

2. Write down a Python code for the numerical integration and analytical integration of

f(x) = a*cos(x) + b*sin(x) + c*exp(-x) + d*x²

from x1 to x2. Run the code and include the source code and the result of code run in your homework.

(Homework 06주)

1. Copper wire: diameter 2 mm, length 10 mm, 10 V applied at both ends. Find a) current, b) current density, and c) electron drift velocity.

2. Line charge at a < xs < b, ys = 0, zs = 0. Field point at (x, y, z). Write down a Python code for calculating the potential by numerical integration and by analytic formula. Run the code and include the source code and the result of code run in your homework.

(Homework 07주)

1. A point charge: q₁ = 10⁻⁹ C at (x, y, z) = (1, 2, 3) m

Another point charge: q₂ = 10⁻¹⁰ C at (x, y, z) m (x, y, z 미지정, 임의값을 넣어서 풀으면 됨.)

Find the store energy

2. Write down a Python code for the stored energy for N point charges.

Input data:

N : number of point charges

qi (C), (xi, yi, zi) m : i-th point charge and position

Output data:

W (J): stored energy

(Homework 08주) Mid-term exam.

(Homework 09주)

(과제) 참고 a_y: unit vector in +y direction.

PIN = abcd: 휴대전화 끝 4 자리 (예: 010-8028-3194, a = 3, b = 1, c = 9, d = 4), 단 각 숫자가 0인 경우 순차적으로 1, 2, 3, 4로 대체 (예: 010-1234-0097인 경우 a = 1, b = 2, c = 9, d = 7)

1. A charge of b C is moving with a velocity of u = a a_y m2/ in a magnetic flux density B = c a_z T, find the force on the charge.

2. Given an infinitesimal current element IdL = a a_z (A·m) at (x, y, z) = (b, c, d), find the magnetic field H at (x, y, z) = (d, c, b) m.

3. Python coding: Write a Python code for calculating B (magnetic flux density) at a distance r from an infinitely long wire current I. Run your code and include the result in your homework.

(Homework 10주)

1. Python coding: Write a Python code for the coding example in the lecture slide.

(Homework 11주)

1. Magnetic field in air is given by H = 2cos(3t + π)a_z (A/m). A 10-turn conducting loop of radius 1 m is placed on the xy plane. Find the voltage V_m induced in the loop.

(Homework 12주)

1. Python coding: Write a Python code for the coding example in the lecture slide.

(Homework 13주)

1. Python coding: Write a Python code for the coding example in the lecture slide.

(Homework 14주)

1. 문제풀이 (Solutions to Problems in Lectures 9 to 13) 중 1문제 선택하여 자신의 PIN을 넣고 풀어서 제출. PIN 사용방법은 자유롭게 하되 숫자 4개 중 3개 이상 사용. 숫자가 0인 경우 순차적으로 1, 2, 3, 4로 대체.

2. 문제풀이 (Solutions to Problems in Lectures 9 to 13) 중 1문제 선택하여 Python으로 계산하는 프로그램 작성하고 소스코드와 실행결과 제출 (강의노트 코딩 예제를 푸는 것이 아님.)

(Homework 15주) Final exam.

[참고자료]

1. Greek alphabet

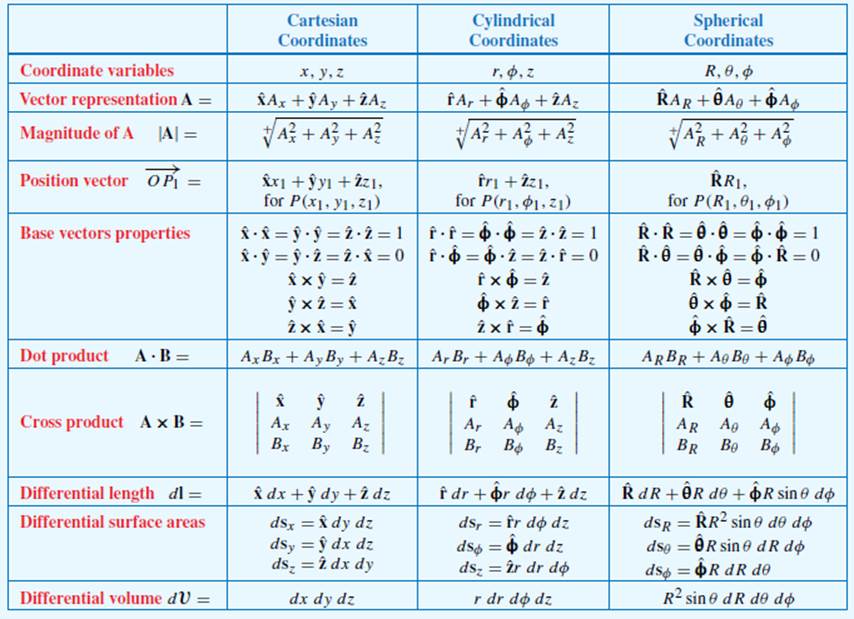
2. Cartesian, cylindrical, spherical coordinates systems and vectors